Bin Liquidity

Introduction

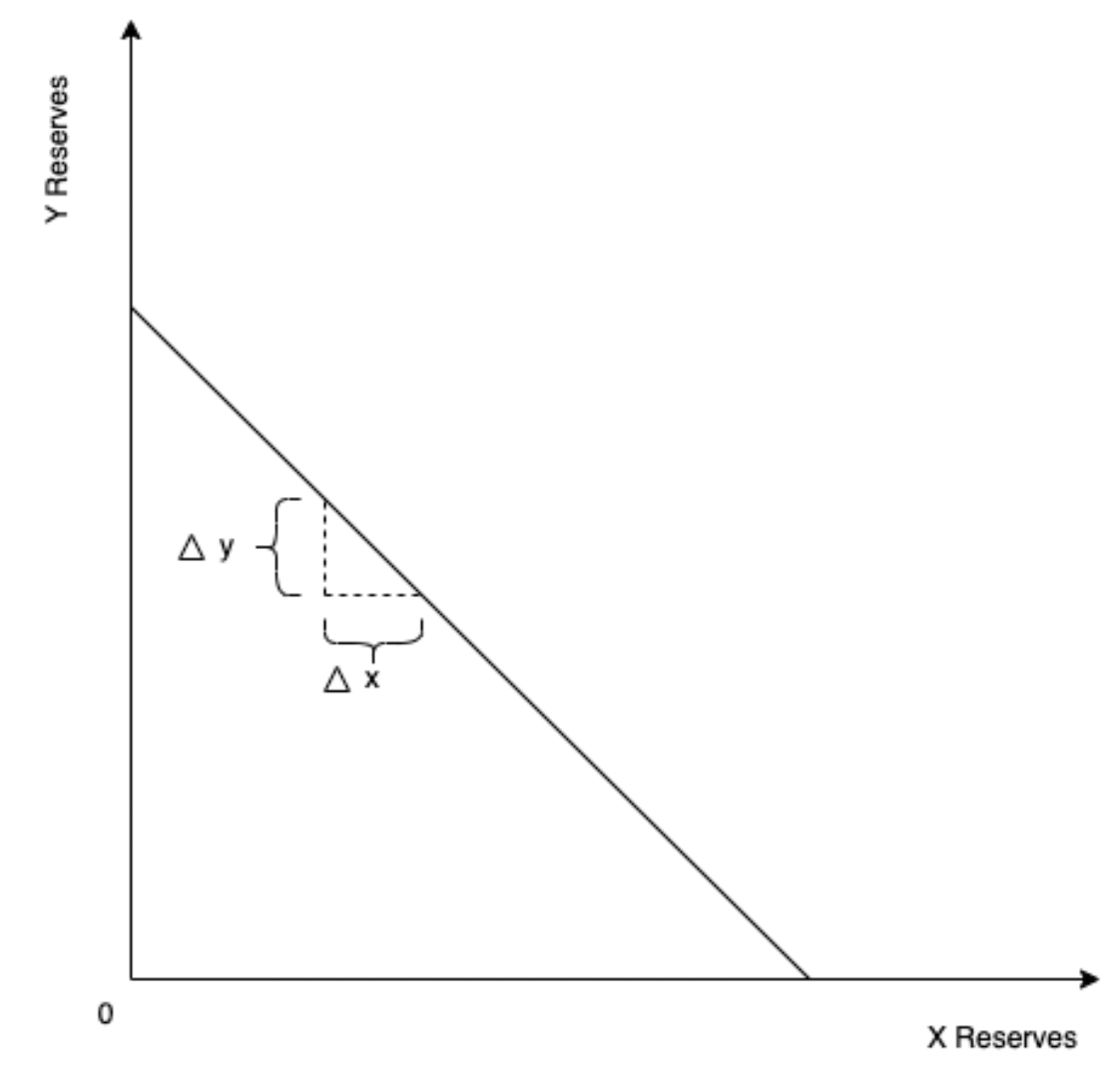
Liquidity in each bin is guided by the constant sum price invariant, $P \cdot x + y = L$, where $x$ is the quantity of asset $X$, $y$ is the quantity of asset $Y$, $L$ is the amount of liquidity in the bin and $P$ is the price defined by $P = \frac{\Delta y}{\Delta x}$. This is more easily visualised by the graph below:

Bin Composition

Since $P$ is the gradient of the line, it is always constant within each bin.

However, unlike the constant product formula, which you may be used to from other AMMs, the price is decoupled from the reserve states of $X$ and $Y$. Put differently, given a price $P$ and a known amount of $x$ (or $y$), you cannot find $y$ (or $x$). In constant product this is possible by simply taking $y = \frac{P}{x}$.

Given that the composition of reserves, $x$ and $y$, are independent of both price and liquidity, an additional variable is used describe the reserves available in the bin. This variable, composition factor ($c$), is the percentage of bin liquidity composing of $y$:

$$c \equiv \frac{y}{L}$$

From this equation, we can deduce $x$ and $y$ as follows:

$$y = cL$$

$$x = \frac{L}{P}(1 - c)$$

Market Aggregation

Another notable difference is that the constant sum curve intercepts both the $x$ and $y$ axes. This means the reserves of $X$ or $Y$ can be depleted. In such a case, the current price moves to the next bin (either to the left or right).

In fact, in any given market, there can only be one bin that contains reserves of both $X$ and $Y$ - this is the active price bin. All bins to the right of the active bin will contain only $X$ and all bins to the left will only contain $Y$.

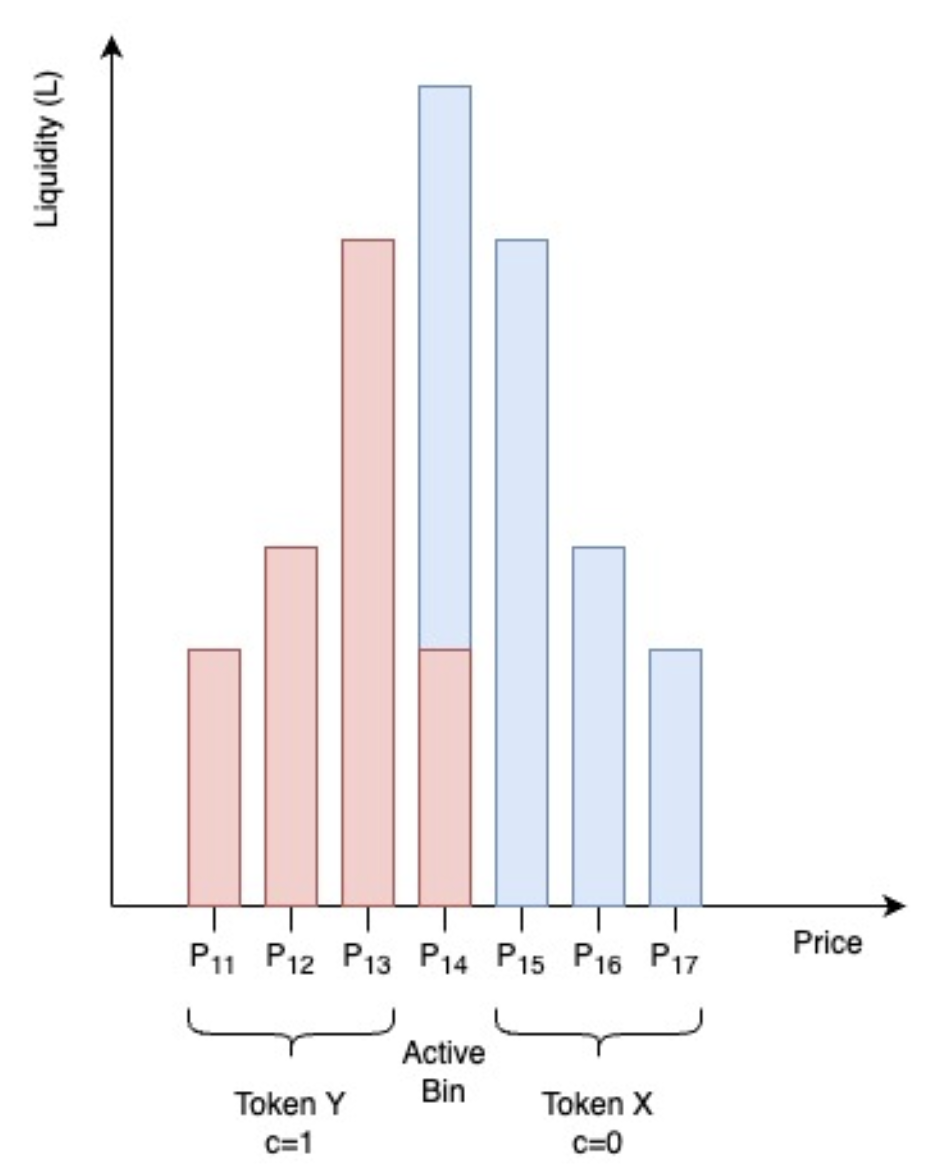
A simple way to think of this is to imagine the MAS/USDC pool. Let asset $Y$ be USDC and asset $X$ be MAS. Price $P$ is defined by amount of USDC per MAS. Let the active bin be $1 MAS; all bins to the left contain only USDC and all bins to the right contain only MAS. If there is a lot of buying of MAS, then the active bin will move to the right once reserves of MAS is depleted from the $1 bin.

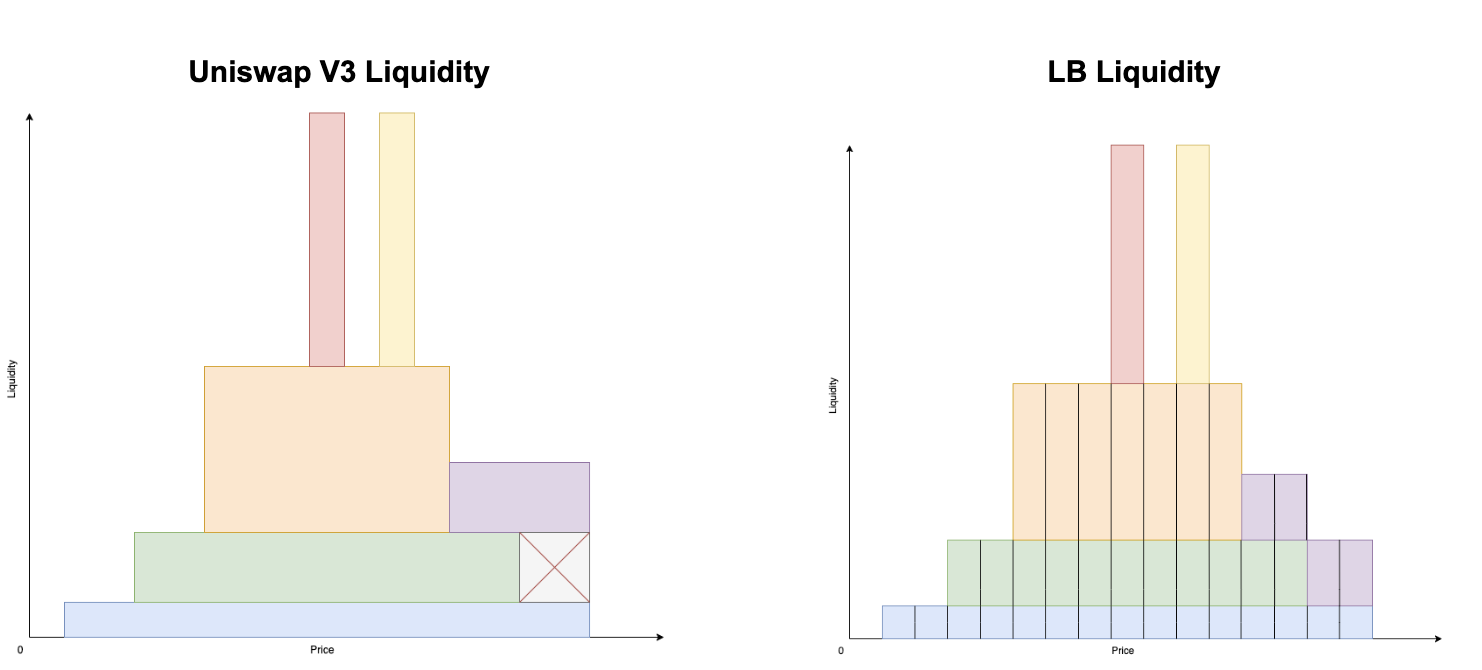
The way LB aggregates liquidity is also different to Uniswap V3. In LB, liquidity is aggregated vertically via each bin and in Uniswap V3, liquidity is aggregated horizontally. The main benefit of vertical aggregation is that it allows for liquidity to be fungible.

Liquidity Tokens

LB introduces a new token standard, LBToken, as the receipt token for liquidity positions.

LBToken tracks the amount of liquidity added to each bin for each user in a given pair. For all intensive purposes, it is almost the same as an ERC-1155 token, but without the functions and variables that are related to NFTs. This makes LBToken fungible, which allows vaults/farms to be easily built on top.

Liquidity Tracking

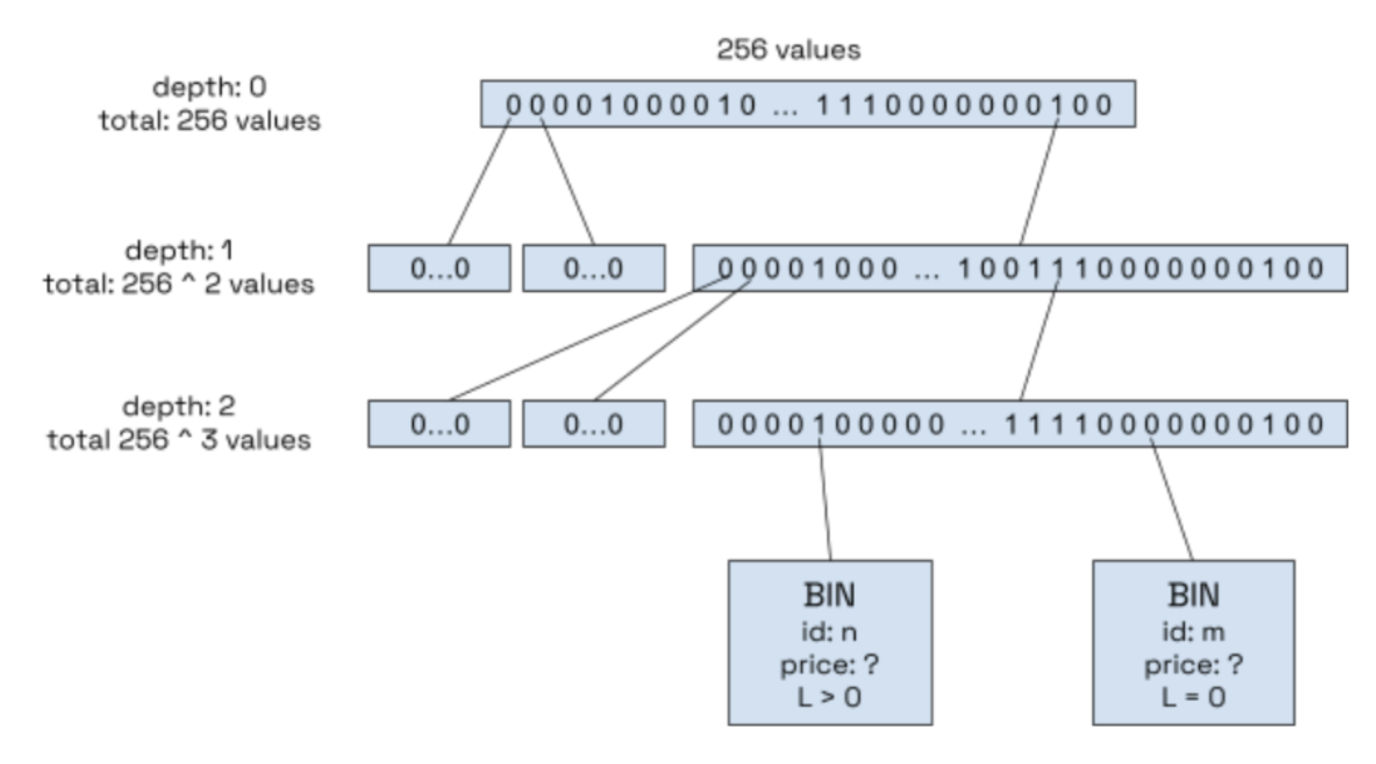
To track liquidity, we use a three level trie in which each node is a 256 bit array represented by a u256. The bottom level, depth 2, contains $256^3 = 16,777,216$ slots, which contains exactly the maximum possible number of bins, $2^{24}$.

When a bin has liquidity, its slot will contain a 1, otherwise it contains a 0. If it contains a 1, then the corresponding slot in its parent will also contain a 1, and likewise, so will the corresponding slot in its grandparent.

Since we always know which bin is the active bin, using a tree structure allows us to find the next bin to its left or right that has liquidity quickly by tracking a path via its parent.